Is Domain All Real Numbers

Real numbers are simply the combination of rational and irrational numbers, in the number system. In general, all the arithmetic operations can be performed on these numbers and they can be represented in the number line, too. At the same fourth dimension, the imaginary numbers are the un-real numbers, which cannot exist expressed in the number line and are commonly used to represent a complex number. Some of the examples of real numbers are 23, -12, 6.99, v/2, π, and so on. In this article, we are going to discuss the definition of real numbers, the properties of real numbers and the examples of existent numbers with consummate explanations.

Table of contents:

Definition
Gear up of real numbers
Nautical chart
Properties of Existent Numbers
- Commutative
- Associative
- Distributive
- Identity
Solved Examples
Practise Questions
FAQs

Real Numbers Definition

Real numbers can exist defined equally the marriage of both rational and irrational numbers. They tin be both positive or negative and are denoted by the symbol "R". All the natural numbers, decimals and fractions come under this category. See the figure, given beneath, which shows the classification of real numerals.

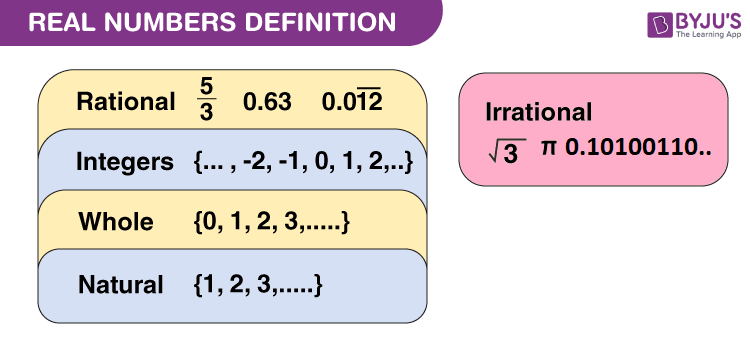
Real numbers definition

Read More:

Natural Numbers And Whole Numbers
Rational And Irrational Numbers
Integers
Real Numbers For Class ten
Important Questions Form 10 Maths Chapter ane Real Numbers

Set of Real Numbers

The gear up of existent numbers consists of different categories, such every bit natural and whole numbers, integers, rational and irrational numbers. In the table given beneath, all the existent numbers formulas (i.e.) the representation of the classification of real numbers are divers with examples.

Category	Definition	Example
Natural Numbers	Contain all counting numbers which start from i. N = {one, two, 3, 4,……}	All numbers such equally 1, 2, three, 4, 5, half-dozen,…..…
Whole Numbers	Collection of zippo and natural numbers. Due west = {0, ane, 2, 3,…..}	All numbers including 0 such as 0, 1, 2, three, iv, 5, half-dozen,…..…
Integers	The collective result of whole numbers and negative of all natural numbers.	Includes: -infinity (-∞),……..-4, -3, -2, -1, 0, ane, 2, 3, 4, ……+infinity (+∞)
Rational Numbers	Numbers that can be written in the grade of p/q, where q≠0.	Examples of rational numbers are ½, 5/four and 12/6 etc.
Irrational Numbers	The numbers which are not rational and cannot exist written in the course of p/q.	Irrational numbers are non-terminating and not-repeating in nature like √2.

Byjusclasses

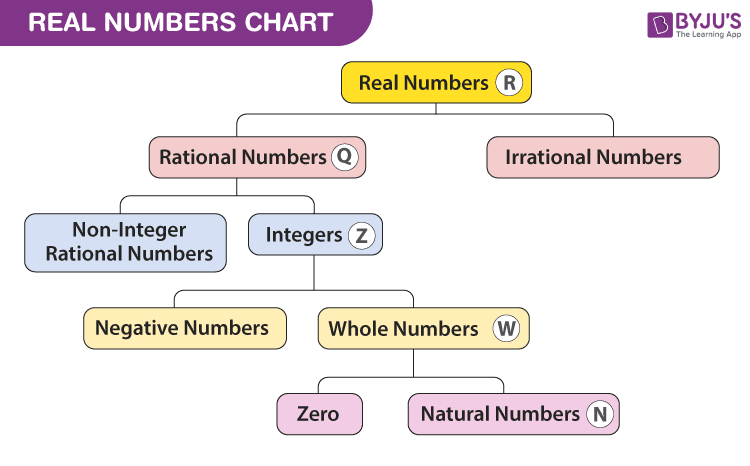
Existent Numbers Chart

The chart for the set of existent numerals including all the types are given beneath:

Real Numbers Chart

Properties of Real Numbers

The following are the four principal properties of existent numbers:

Commutative property
Associative property
Distributive belongings
Identity property

Consider "chiliad, n and r" are three existent numbers. So the above properties tin can be described using k, n, and r every bit shown below:

Commutative Holding

If m and northward are the numbers, then the general class will exist thousand + n = n + m for addition and m.n = n.grand for multiplication.

Addition: grand + n = n + m. For example, 5 + three = iii + 5, 2 + 4 = 4 + 2.
Multiplication: m × northward = north × thou. For example, v × 3 = 3 × 5, 2 × 4 = four × 2.

Associative Holding

If thou, due north and r are the numbers. The general form volition be thousand + (due north + r) = (m + due north) + r for addition(mn) r = m (nr) for multiplication.

Addition: The general form will exist m + (n + r) = (m + north) + r. An example of additive associative belongings is ten + (3 + ii) = (10 + 3) + two.
Multiplication: (mn) r = m (nr). An example of a multiplicative associative property is (2 × 3) iv = 2 (three × iv).

Distributive Property

For 3 numbers m, n, and r, which are real in nature, the distributive property is represented as:

g (due north + r) = mn + mr and (m + n) r = mr + nr.

Example of distributive belongings is: 5(2 + 3) = five × 2 + 5 × 3. Here, both sides will yield 25.

Identity Belongings

In that location are condiment and multiplicative identities.

For improver: m + 0 = yard. (0 is the condiment identity)
For multiplication: one thousand × i = 1 × grand = m. (one is the multiplicative identity)

Video Lesson on Numbers

Solved Examples

Example i:

Discover five rational numbers between 1/2 and 3/five.

Solution:

We shall make the denominator same for both the given rational number

(ane × v)/(two × v) = five/10 and (3 × 2)/(5 × two) = half dozen/10

At present, multiply both the numerator and denominator of both the rational number by 6, we have

(5 × 6)/(10 × half dozen) = 30/lx and (half dozen × six)/(10 × half-dozen) = 36/60

Five rational numbers betwixt i/2 = 30/sixty and three/5 = 36/threescore are

31/threescore, 32/lx, 33/60, 34/sixty, 35/60.

Instance 2:

Write the decimal equivalent of the following:

(i) 1/iv (two) five/8 (iii) 3/2

Solution:

(i) 1/iv = (ane × 25)/(iv × 25) = 25/100 = 0.25

(ii) 5/viii = (5 × 125)/(eight × 125) = 625/1000 = 0.625

(iii) 3/2 = (three × v)/(2 × five) = xv/10 = i.v

Example 3:

What should exist multiplied to one.25 to get the answer 1?

Solution: 1.25 = 125/100

Now if we multiply this by 100/125, we get

125/100 × 100/125 = 1

Practice Questions

Which is the smallest composite number?
Prove that any positive odd integer is of the course 6x + 1, 6x + 3, or 6x + 5.
Evaluate two + 3 × 6 – v.
What is the product of a not-zero rational number and an irrational number?
Can every positive integer be represented every bit 4x + 2 (where x is an integer)?

Real Numbers Class 9 and 10

In existent numbers Grade 9, the common concepts introduced include representing real numbers on a number line, operations on existent numbers, backdrop of real numbers, and the law of exponents for real numbers. In Course x, some advanced concepts related to real numbers are included. Apart from what are real numbers, students will as well acquire nigh the existent numbers formulas and concepts such equally Euclid'due south Partitioning Lemma, Euclid's Segmentation Algorithm and the primal theorem of arithmetics in course ten.

Proceed visiting BYJU'Due south to get more such Maths lessons in a simple, concise and easy to empathize way. Also, register at BYJU'Southward – The Learning App to get complete assistance for Maths grooming with video lessons, notes, tips and other study materials.

Frequently Asked Questions on Real Numbers

What are Natural and Existent Numbers?

Natural numbers are all positive integers starting from one to infinity. All natural numbers are integers but not all the integers are natural numbers. These are the set of all counting numbers such as 1, 2, 3, 4, v, 6, seven, 8, 9, …….∞.

Real numbers are numbers that include both rational and irrational numbers. Rational numbers such equally integers (-two, 0, 1), fractions(i/2, 2.5) and irrational numbers such as √iii, π(22/7), etc., are all real numbers.

Is Zero a Existent or an Imaginary Number?

Zero is considered to be both a real and an imaginary number. Every bit nosotros know, imaginary numbers are the square root of non-positive real numbers. And since 0 is as well a non-positive number, therefore it fulfils the criteria of the imaginary number. Whereas 0 is also a rational number, which is divers in a number line and hence a existent number.

Are there Existent Numbers that are not Rational or Irrational?

No, in that location are no real numbers that are neither rational nor irrational. The definition of real numbers itself states that it is a combination of both rational and irrational numbers.

Is the real number a subset of a circuitous number?

Yeah, because a complex number is the combination of a existent and imaginary number. And so, if the circuitous number is a set then the real and imaginary numbers are the subsets of it.

What are the backdrop of real numbers?

The properties of real numbers are:
Commutative Property
Associative Holding
Distributive Property
Identity Property

Is √3 a real number?

Yep, √3 is a real number. Nosotros know that a real number is a combination of both rational and irrational numbers. Since √3 is an irrational number, we tin besides say that √3 is a existent number.

Is 3i a existent number?

No, 3i is not a real number, as it has an imaginary function in it.

What are the unlike subsets of existent numbers?

The subsets of existent numbers include rational numbers, irrational numbers, natural numbers, and whole numbers.